Bài 3 trang 125 SGK Toán 4

Bài 3 trang 125 sgk Toán 4 được giải và chia sẻ với mục đích giúp các phụ huynh tham khảo cách làm, đáp án để có thể hỗ trợ các em học sinh ôn tập và rèn luyện lại kiến thức đã học trên lớp.

Giải bài 3 trang 125 SGK Toán 4

Đề bài

Cho hình chữ nhật \(ABCD\) có chiều dài \(12cm\), chiều rộng \(5cm\). Nối đỉnh \(A\) với trung điểm \(N\) của cạnh \(DC\). Nối đỉnh \(C\) với trung điểm \(M\) của cạnh \(AB\). Cho biết hình tứ giác \(AMCN\) là hình bình hành có chiều cao \(MN\) bằng chiều rộng hình chữ nhật.

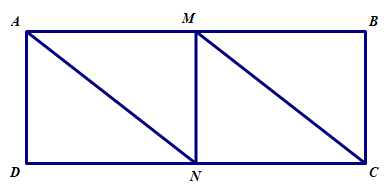
a) Giải thích tại sao đoạn thẳng \(AN\) và \(MC\) song song và bằng nhau.

b) Diện tích hình chữ nhật \(ABCD\) gấp mấy lần diện tích hình bình hành \(AMCN\)?

Hướng dẫn

Bài Giải

a) Các đoạn thẳng \(AN\) và \(MC\) là hai cạnh đối diện của hình bình hành \(AMCN\) nên chúng song song và bằng nhau.

b) Diện tích hình chữ nhật \(ABCD\) là:

\(12 \times 5 = 60\,(cm^2) \)

Vì \(N\) là trung điểm của cạnh \(DC \) nên độ dài đoạn thẳng \(NC\) là:

\(12 : 2 = 6\, (cm)\)

Hình bình hành \(AMCN\) có chiều cao \(MN\) bằng chiều rộng hình chữ nhật nên \(MN = 5cm\).

Diện tích hình bình hành \(AMCN\) là :

\(6 \times 5 = 30\, (cm^2) \)

Ta có: \(60 : 30 = 2\)  (lần)

Vậy diện tích hình chữ nhật \(ABCD\) gấp 2 lần diện tích hình bình hành \(AMCN\).

» Bài tiếp theo: Bài 1 trang 126 sgk Toán 4

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 3 trang 125 sgk toán 4. Mong rằng những bài hướng dẫn giải Toán 4 của ĐọcTàiLiệu sẽ là người đồng hành giúp các em học tập thêm hiệu quả và tư duy hơn sau khi học trong SGK.